Recommenders with Deep Learning

Learned Embeddings

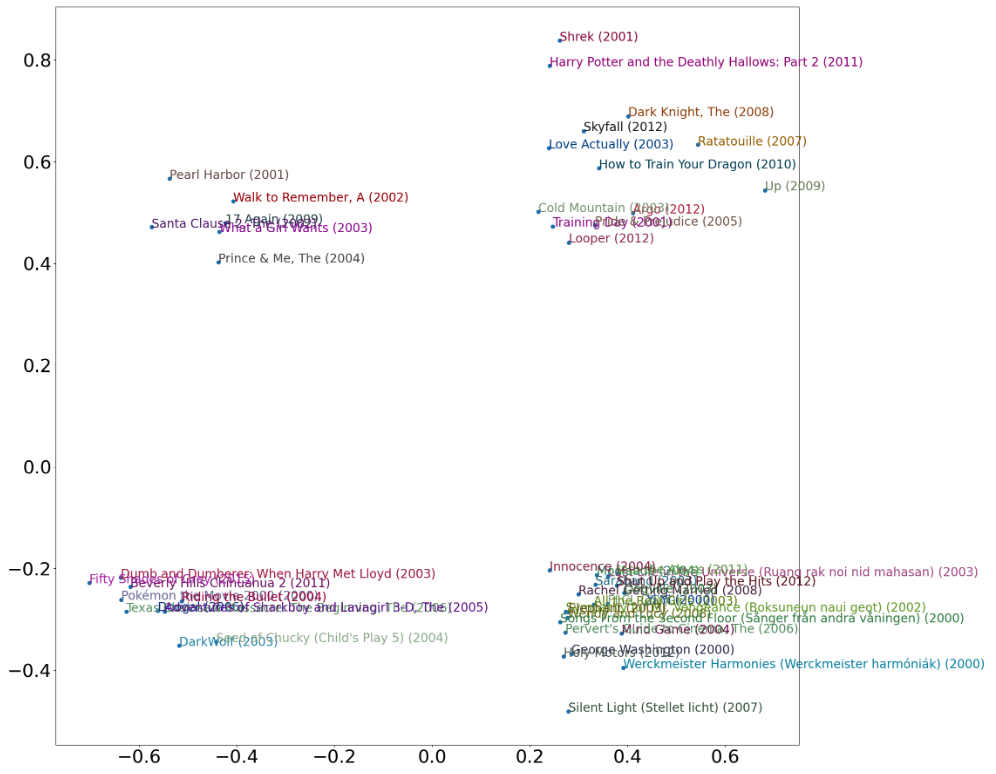
First and Second principal components of embeddings

We see even without genre as a feature in model or age restriction rating, the embeddings have learnt the following concepts (rough interpretation of latent features):

Chick Flicks VS. Mass Appeal on PCA 1 (x-axis)

• Chick Flicks - A Walk to Remember, The Prince & Me, Fifty Shades of Grey, 17 Again
• Mass Appeal - Dark Knight, Skyfall, Ratatouille

Kids & Family VS. Restricted on PCA 2 (y-axis)

• Kids & Family - Shrek, Harry Potter, How to Train Your Dragon, Santa Clause 2, Up
• Restricted - Fifty Shades of Grey, Texas Chainsaw Massacre, Seed of Chucky

# Principal Component Analysis to represent movie embeddings in 2-D
from sklearn.decomposition import PCA
from matplotlib import pyplot
X = model.m_emb.weight.data
pca = PCA(n_components=2)
result = pca.fit_transform(X)

Network Architecture

# Make a neural network
class Model(nn.Module):
  def __init__(self, n_users, n_items, embed_dim, n_hidden=1024):
    super(Model, self).__init__()
    self.N = n_users
    self.M = n_items
    self.D = embed_dim

    self.u_emb = nn.Embedding(self.N, self.D)
    self.m_emb = nn.Embedding(self.M, self.D)
    self.fc1 = nn.Linear(2 * self.D, n_hidden)
    self.fc2 = nn.Linear(n_hidden, 1)

    # set the weights since N(0, 1) leads to poor results
    self.u_emb.weight.data = nn.Parameter(
        torch.Tensor(np.random.randn(self.N, self.D) * 0.01))
    self.m_emb.weight.data = nn.Parameter(
        torch.Tensor(np.random.randn(self.M, self.D) * 0.01))
  
  def forward(self, u, m):
    u = self.u_emb(u) # output is (num_samples, D)
    m = self.m_emb(m) # output is (num_samples, D)

    # merge
    out = torch.cat((u, m), 1) # output is (num_samples, 2D)

    # ANN
    out = self.fc1(out)
    out = F.relu(out)
    out = self.fc2(out)
    return out

Model(
  (u_emb): Embedding(671, 10)
  (m_emb): Embedding(9066, 10)
  (fc1): Linear(in_features=20, out_features=1024, bias=True)
  (fc2): Linear(in_features=1024, out_features=1, bias=True)
)

Recommender Accuracy using Embeddings & ANN

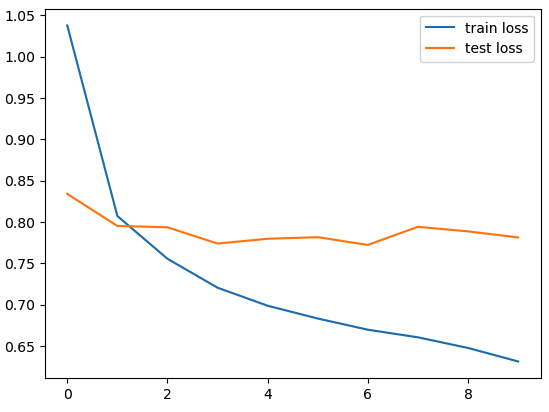
The ANN RMSE of 0.8839 is even lower than SVD++ RMSE of 0.8928 on the MovieLens 100K ratings dataset. Also, the power of deep learning is with large datasets and to test this, I ran the model additionally on MovieLens 20M ratings dataset to get an RMSE of 0.7941.

Epoch 1/10, Train Loss: 1.0377, Test Loss: 0.8340, Test RMSE: 0.9132, Duration: 0:00:00.694932
Epoch 2/10, Train Loss: 0.8072, Test Loss: 0.7952, Test RMSE: 0.8917, Duration: 0:00:00.736841
Epoch 3/10, Train Loss: 0.7554, Test Loss: 0.7935, Test RMSE: 0.8908, Duration: 0:00:00.683794
Epoch 4/10, Train Loss: 0.7204, Test Loss: 0.7739, Test RMSE: 0.8797, Duration: 0:00:00.660207
Epoch 5/10, Train Loss: 0.6986, Test Loss: 0.7796, Test RMSE: 0.8830, Duration: 0:00:00.622400
Epoch 6/10, Train Loss: 0.6831, Test Loss: 0.7816, Test RMSE: 0.8841, Duration: 0:00:00.655083
Epoch 7/10, Train Loss: 0.6696, Test Loss: 0.7722, Test RMSE: 0.8787, Duration: 0:00:00.648430
Epoch 8/10, Train Loss: 0.6604, Test Loss: 0.7941, Test RMSE: 0.8911, Duration: 0:00:00.627179
Epoch 9/10, Train Loss: 0.6475, Test Loss: 0.7886, Test RMSE: 0.8880, Duration: 0:00:00.641276
Epoch 10/10, Train Loss: 0.6312, Test Loss: 0.7812, Test RMSE: 0.8839, Duration: 0:00:00.628338

Recommendations using Deep Learning

We recommend: 

Singin' in the Rain (1952)
Princess Bride, The (1987)
Henry V (1989)
Name of the Rose, The (Name der Rose, Der) (1986)
Lock, Stock & Two Smoking Barrels (1998)
Grand Illusion (La grande illusion) (1937)
Dog Day Afternoon (1975)
Lilo & Stitch (2002)
Band of Brothers (2001)
Midnight in Paris (2011)